Sur Matchafa: Le système bancaire à réserve fractionnelle - la privatisation de l’argent

.
Sur Matchafa: Le système bancaire à réserve fractionnelle - la privatisation de l’argent

Voilà un autre confrère québécois qui s'est penché sur le fonctionnement du système bancaire fractionnaire. J'en ai parlé à plusieurs reprises, autant sur LNI que sur L'Autre Monde, car c'est probablement le sujet le plus important et le plus préoccupant. Ne manquez pas la rubrique "système bancaire" du site.

Avec un recul de recherches depuis dix ans, je peux m'avancer en toute confiance en vous disant que c'est le coeur de la majorité de nos problèmes économiques avec tout ce que cela implique, jusqu'au niveau politique (Évidemment qu'il faudrait placer la nature de l'homme et de ses fausses motivations au coeur). Je suis très heureux de vous présenter cette série laborieuse qui a dû demander une somme de travail et d'analyse considérable, sans compter le talent pour le synthétiser. Cette série complètement très bien toute la section du système bancaire de ce site.

Ne manquez pas de visiter le site de Matchafa!

La privatisation de l’argent: une introduction

22 11 2007

Après avoir discuter avec certaines personnes, dont certains banquiers, à propos de la fraude qu’est le système bancaire à réserve fractionnelle et m’être vu répondre en premier lieu que «c’était normal», je me suis rendu compte que si même les banquiers ne voient pas l’ampleur de la fraude à moins d’être présenté avec un exemple vraiment flagrant, je ne peux pas m’attendre à ce que tout le monde puisse voir la fraude pour ce qu’elle est sans que je donne un exemple vraiment flagrant. Donc, avant de procéder à la partie III de la série (à propos de l’inflation et des cycles économiques), je vais rajouter une introduction (le présent billet) à la partie I, qui sera simplement un exemple flagrant, un exemple presque caricatural: l’exemple du Canada.

Mais avant il convient de reprendre, en quelques mots l’analogie de l’île. Admettons qu’une dizaine de personnes décident de s’établir sur une île déserte afin de bâtir une communauté. Ils sont arrivés avec beaucoup de matériel pour construire leur île mais qu’avec très peux d’argent: seulement la monnaie qui s’adonnait à se trouver dans leur portefeuille. Ils réalisent donc très vite qu’ils vont devoir créer de l’argent afin de satisfaire à leurs échanges économiques. Une personne, appelons-la Sophie, propose une solution: elle va imprimer de l’argent chez elle et va le prêter, moyennant intérêts, à tout ceux et celles dans lesquels elle aura confiance d’être repayée. Si vous étiez une des personnes de l’île (autre que Sophie) serriez vous d’accord avec ce marché? J’espère croire que toute personne sensée refuserait cette arnaque pas très subtile. Et pourtant, c’est exactement le système mis en place à peu près partout dans le monde!

Le Canada, le «plusse meilleur pays au monde», est un exemple particulièrement flagrant parce qu’il n’y a pas de taux de réserve minimale. Ceci veut dire la chose suivante. Je peux être complètement fauché, mais si j’obtiens l’autorisation du ministère d’ouvrir ma banque, sans avoir une seule cenne (centime pour les utilisateurs/rices de francs), je peux commencer à prêter de l’argent, pire encore, il n’y a pas de limite sur la quantité d’argent que je peux prêter. C’est pas des blagues, j’ai vraiment aucun argent, même pas l’argent de quelqu’un d’autre qui aurait déposé de l’argent chez ma banque, zéro, nada, niet, pas une cenne, mais je peux prêter autant d’argent que je veux. L’argent que je prête c’est de l’argent virtuel que je crée de toutes pièces, je ne fais qu’inscrire le montant au compte de la personne qui emprunte. Sur ce «prêt» que je fournie à la malheureuse personne qui m’emprunte de l’argent je demande des intérêts qui peuvent varier entre 6% pour un prêt hypothécaire à 30% pour les cartes de crédit* les plus usurières (au Canada). Mais d’un autre coté, l’argent que je crée de toutes pièces est bien réelle dans le sens que peux acheter ce que je veux avec: je peux acheter une voiture si je le veux, sans avoir une cenne, je n’ai qu’à inscrire le montant au compte du concessionnaire automobile. Mais, comme je suis une banque, la majorité de l’argent que je crée sert à faire des prêts aux gens. Notez aussi que si j’ai pas d’argent pour commencer mais je prête un million de dollars à quelqu’un, j’inscris ce montant dans son compte et donc, dans mon livre comptable j’ai 1 million de dollars de dépôts et un million de dollars de prêts, donc superficiellement on dirait que je prête l’argent que les gens déposent chez ma banque! Cette exemple n’est pas juste un exemple farfelu, la quasi-totalité de l’argent créé (95% environ) au Canada (et dans la majorité des autres pays) l’est par les banques, exactement de la même manière qu’illustré par mon hypothétique banque qui commence sans le sou.

En fait, c’est comme une taxe, collectivement, on paie plus de 6% d’intérêts sur tout l’argent en existence au pays! Pour tout dollar en existence, il y a quelqu’un qui paie de l’intérêt dessus! En fait on peu même le vérifier facilement l’exactitude de cette affirmation. Selon la Banque du Canada, en 2006, il y avait environ 1000 milliards de dollars en circulation au Canada (incluant les devises étrangères), dont seulement environ 46 milliards en argent comptant hors des banques (argent créé par la Banque du Canada). Parallèlement, en regardant sur Reuters et les sites respectifs des banques ont voit que collectivement, la CIBC, la Banque de Montréal, TD, la Banque de Nouvelle-Écosse, la Banque Royale, la Banque Nationale, les Caisses Desjardins et la Banque Laurentienne (les banques privés [car c'est pratiquement ce que Desjardins est devenu] ayant les plus grosses parts de marché au Canada), ont récoltés 87 milliards de dollars en intérêts**. Si ont suppose que les banques mentionnée ci haut ont collectivement 100% des parts du marché, ça veut dire que collectivement, nous payons 8,7% d’intérêt par année sur toute l’argent en circulation.

Nous payons une taxe de 8,7% par année aux banques privés pour utiliser les dollars canadiens créés par les banques privées. Mais cette taxes fonctionne à l’inverse de la l’impôt sur le revenu avec lequel nous sommes familiers. En effet, l’impôt sur le revenu est gradué de façon que les pauvres n’en paient presque pas tandis que les riches en paient (ou du moins seraient censé payer s’il n’y avait pas de paradis fiscaux) une portion croissante de leurs revenus. Pour la taxe sur l’argent c’est le contraire, les pauvres qui n’arrivent même pas à payer leur facture de carte de crédit paient un taux d’environ 20% sur l’argent qu’ils utilisent, tandis que les riches qui ont trop d’argent reçoivent un «remboursement de taxe» d’environs 5% sur l’argent qu’ils ont.

Comparons cette taxe perçoivent les banques sur la création de l’argent aux taxes et impôts des gouvernements. Le gouvernement fédéral a perçu environs 200 milliards de dollars en taxes, impôts et cotisations de toutes sortes en 2006 (ceci n’inclue pas les revenus des sociétés d’État ou des activités de l’État), de ce montant, 33 milliards étaient utilisés pour payer les intérêts sur la dette. Ceci veut dire qu’en 2006 nous avons payé 167 milliards de dollars pour les services du gouvernement fédéral*** comparé à 87 milliards de dollars en taxes pour le droit d’utiliser l’argent créé par les banques. Cela veut dire qu’un tiers [87/(87+167)*100% = 34% ] de nos «taxes» servent à payer les banques pour le droit d’utiliser l’argent qu’elles crée. Regardons les choses d’une perspective. Admettons que l’argent est créé par le gouvernement au lieu d’être créé par les banques, déjà le gouvernement n’aurait pas besoin d’emprunter donc il n’aurait pas de dette et donc n’aurait pas à payer 33 milliards pour servir la dette mais en plus, au cours de 2006, les banques ont créé environ 100 milliards de dollars donc si gouvernement était celui qui créait l’argent, il aurait eu, en 2006, 100 milliards de dollars de plus qu’il aurait créé à la place des banques et donc aurait besoin de collecté 100 milliards de dollars de moins en taxes et impôts. Ce qui fait, qu’au lieu de collecter 200 milliards de dollars en taxes et impôts comme le gouvernement du Canada l’a fait en 2006, il aurait pu collecté seulement 67 milliards de dollars en taxes et impôts et fournir exactement les mêmes services! Ceci représente un rabais de 67% sur les taxes et impôts collectés!

J’imagine qu’à ce point-ci vous vous demandez, si c’est si profitable d’être une banque, pourquoi est-ce qu’il n’y a pas de gens qui fondent des banques au lieu de faire autre chose. «C’est quoi la pogne?» En fait, collectivement les banques sont très profitables, mais individuellement ce n’est pas nécessairement le cas. Toute la profitabilité usurière repose sur l’hypothèse que les banques peuvent prêter de l’argent qu’elles créent. Cela peut seulement se faire si les gens qui emprunte de l’argent ne demandent pas d’avoir leur argent en main propre ou ne transfère pas cet argent vers un autre banque, i.e. l’argent qui est prêté par la banque reste dans cette banque, la banque récolte alors de l’intérêt sur l’argent mais elle n’a pas a fournir l’argent. Ceci n’est pas un problème pour une grosse banque car si elle prête 100 000 $ à quelqu’un, même si la personne dépense son 100 000$ d’un coup, il y a de grosses chances que la personne qui reçoit les 100 000$ va encaisser son chèque dans son compte chez la même grosse banque et donc l’argent ne sortira jamais de cette banque, la banque n’aura jamais à vraiment fournir l’argent. Et même si la personne qui reçois le 100 000$ va le déposer chez une autre banque, en moyenne il y aura quelqu’un d’autre qui déposera un 100 000$ provenant de la seconde banque dans un compte de la première banque, ce qui rééquilibra la chose et ferra en sorte qu’aucune banque ne fournira réellement d’argent. En pratique les grandes banques n’ont besoins que de 2-3% de tout l’argent qu’elles prêtent pour satisfaire à la demande. Mais évidemment s’il y a un flux net d’argent d’une banque vers une autre, la banque déficitaire devra emprunter l’argent qui lui manque ce qui aura pour effet qu’elle récoltera de l’intérêt non pas sur de l’argent qu’elle a créé mais sur de l’argent qu’elle a emprunté. Cela et largement moins profitable et si le transfert d’argent se fait trop vite, la banque n’aura pas le temps d’emprunter assez d’argent pour répondre à ses obligations et sera forcée de faire faillite. Ce genre de situation est beaucoup plus probable pour une petite banque. Mais, cela peut arriver même aux grosses banque, si tout le monde allait sortir son argent en argent comptant, toutes les banques ferraient faillite, car collectivement elles possèdent moins de 5% de tout l’argent qui est déposée chez elles. L’autre 95% est de l’argent qu’elles ont créé en faisant des prêts mais qui est resté déposé (pas nécessairement par la même personne) chez les banques.

La majorité des pays ne sont pas comme le Canada, et fonctionnent avec un système bancaire à réserve fractionnelle avec un taux de réserve minimum non nul. Quoi que cela soit mieux en théorie, en pratique cela revient exactement au même simplement parce que c’est toujours les banques privées qui créent la majorité de l’argent. La partie I de cette série parle donc du cas plus général du système bancaire à réserve fractionnelle ou le taux de réserve minimal est arbitraire. Le cas du Canada que l’on vient de considérer est le cas spécifique où le taux est nul. La partie II de la série est une analyse comptable plus détaillée du processus de création d’argent dans un système bancaire de réserve fractionnelle. La partie III traitera de l’inflation et des cycles économiques. Une grande majorité des articles ou médias ou politiciens qui critiquent le système bancaire à réserve fractionnelle préconisent de retourner en arrière et de remettre en place un système monétaire basé sur l’or. La partie IV expliquera pourquoi cela n’est pas la bonne solution et proposeras certaines solutions alternatives. Finalement la partie V fournira des références pour des ressources supplémentaires sur le sujet.

*Visa appartient aux banques membres (quoiqu’elle va bientôt être introduite en bourse) et MasterCard quoique coté en bourse appartient surtout aux banques dont les plus grosses parts appartiennent à Banque of América (11% via Marisco), Fidelity Investements (8%) et Goldman Sachs (4,5%) . Mais, de toute façon, Visa et MasterCard ne sont que fournisseurs de solutions informatiques, ce sont les banques émettrices qui perçoivent l’intérêt sur les dettes de carte de crédit et ce sont les banques qui perçoivent aussi les frais de transactions d’environ 2% (et de 1% environ pour les carte de débit) auprès des commerçant(e)s sur toutes les transactions effectuées par le biais des réseau Visa, MasterCard (et aussi Interac).

**RBC: 22,2 milliards, Scotia: 17,7 milliards, TD: 15,5 milliards, CIBC: 13,2 milliards, BMO: 13 milliards, BN: 4 milliards, Laurentienne: 0,8 milliards, Desjardins: 0,6 milliards.

***Bon d’accord, c’est vrai que je ne vois pas trop l’utilité des «services» du gouvernement fédéral (la guerre en Afghanistan je ne trouve pas que c’est un service qui m’est rendu), mais le problème est que c’est difficile de faire une comparaison avec le gouvernement du Québec puisque je ne peut pas trouver les données de l’intérêt perçu seulement au Québec. Mais juste pour avoir une idée, les revenus du gouvernement du Québec étaient de 55,1 milliards de dollars en 2006 incluant 9,6 milliards de transferts fédéraux et les revenus des sociétés d’États et de ce montant 7 milliards était utilisés pour servir la dette. On peut estimer les intérêts perçus au Québec par les Banque en multipliant les intérêts perçus au Canada par la proportion de l’économie canadienne qui est québécoise: en 2006 le PIB du Québec était de 260 milliards et le PIB du Canada était 1280 milliards, donc le Québec représente à peu près 20% de l’économie canadienne donc on s’attendrait à ce que les banques aient récoltés 20%*87 milliard = 18 milliards de dollars en intérêts. Donc au Québec on a payé une taxe d’environ 18 milliards de dollars pour pouvoir utiliser l’argent créé par les banques [ce montant est à comparer aux 550 millions par année qu'il faudrait pour instaurer la gratuité scolaire à tous les niveaux au Québec] tandis qu’on payait 48 milliards de dollars pour recevoir les services du gouvernement (santé, éducation, transport en commun, etc.) ce qui veut dire que les taxes pour payer l’utilisation de l’argent créé par les banques représentaient 27% du montant total!

Le système bancaire à réserve fractionnelle: la privatisation de l’argent (partie I)

9 08 2007

Ce billet est la suite logique de l’introduction que vous pouvez trouver ici: «La privatisation de l’argent: une introduction».

Qui crée la monnaie? Vous croyez surement, comme la majorité des gens, que c’est votre gouvernement qui crée la monnaie de votre pays. Rien n’est plus faux. La grande majorité de l’argent est créée par des banques privées, environs 95% [7] pour être plus précis (on parle ici de création net d’argent et non pas du renouvèlement des vieux billets par des nouveaux). Autrement dit, seulement environs 5% de l’argent en circulation est créée par votre gouvernement, on comprend mieux alors pourquoi le gouvernement doit continuellement emprunté de l’argent aux frais des contribuables et aux profits des banques! En 1912, comme l’atteste la photo ci-haut, cela était plus visible car les banques privées imprimaient monnaie (et étaient pratiquement les seules à le faire [5]), ce qu’elles ne font plus. L’argent imprimé par les banques privées étaient en circulation au Canada jusqu’en janvier 1950 et ces billets sont encore valide dans le sens que la Banque du Canada est toujours tenue de les accepter et de les échanger pour des nouveau billets ([11] article 26 alinéa 2). Mais, comment les banques privées peuvent créée de l’argent sans en imprimer? C’est ce que nous allons voir.

Le système bancaire à réserve fractionnelle, si simple mais que personne ne comprend

À la base, la création d’argent commence en effet par l’impression de billet papiers et le battage de pièces de monnaie par le gouvernement (à l’exception des États-Unis où, pour créer de l’argent, le gouvernement fédéral doit préalablement s’endetter en émettant des obligations, mais nous ne parlerons pas de cet cas particulièrement frauduleux et nous nous concentrerons plutôt sur le cas générique). Par exemple, au Canada, la Banque du Canada (banque centrale) imprime les billets et peut créer de la monnaie électronique et la Monnaie royale canadienne (société de la Couronne depuis 1969 [6]) bat la monnaie. Une fois cette argent fraichement créée il y a deux façon de la distribuer:

1. Payer les créditeurs de la banque centrale: c’est-à-dire payer les gens qui travaillent à la banque centrale ou eux qui ont vendu de l’or, de l’argent, de l’équipement, de la machinerie, des immeubles, etc. à la banque centrale ([11] article 25 alinéa 1).
2. Échanger cet argent contre d’autres formes d’argent comme par exemple: des devises étrangères, de l’argent électronique créée par des banque privées, des billets de banque imprimées par des banques privées qui étaient en circulation avant 1950 (pour ce qui est du Canada, maintenant ce genre d’échange n’a pas lieu souvent mais en ‘49-’50 la Banque du Canada a converti la majorité des billets de banque privés en l’argent que nous utilisons maintenant), des billets de la Banque du Canada usés, etc.

Et c’est ici que commence la deuxième vague de création de l’argent, celle qui produit la majorité de l’argent: l’argent électronique créée par les banques commerciales. Bien que cette argent soit créée sous forme électronique, elle est toute aussi vraie que l’argent en papier ou en métal, car la banque centrale a l’obligation ([11] art. 26, al. 1-2) d’imprimer assez de billets pour échanger l’argent électronique déposée par une banque privée à la banque centrale en billets de banque de papier.

Mais comment-donc cet argent électronique est-il créé par les banques commerciales? Chaque pays, de par ses lois, défini un taux de réserve T (qui peut changer de temps à autre mais qui est toujours inférieur à 100%), nous utiliserons T=10% par la suite ce qui correspond au taux en vigueur aux États-Unis. Pour connaitre le taux en vigueur dans d’autre pays, référez-vous à la Table 1 colligée d’après [2].
TABLE 1:

Réserves minimales légales Pays Réserve fractionnelle requise (%) Australie 0.00 Canada 0.00 Mexique 0.00 Suède 0.00 Royaume-Uni 0.00 Eurozone 2.00 Slovaquie 2.00 Suisse 2.50 Chili 4.50 Inde 7.00 Bulgarie 8.00 Lettonie 8.00 Burundi 8.50 Hongrie 8.75 Chine 11.50 Pakistan 7.00 Ghana 9.00 États-Unis 10.00 Estonie 15.00 Zambie 17.50 Croatie 19.00 Tadjikistan 20.00 Surinam 35.00 Jordanie 80.00

Exemple: le tour de magie, 100$ dans un chapeau/banque magique devient 1000$

Le principe de base pour que les banques puisse créer de l’argent est le suivant: elle peuvent prêter plus d’argent qu’elles ont dans leurs coffres! Le montant maximal qu’elles ont le droit de prêter est déterminer par le taux de réserve minimal (10% pour le prochain exemple) et le montant d’argent qu’elles ont dans leurs coffres (leurs réserves). Les banques peuvent «créer» et prêter autant argent qu’elles le veulent tant que le ratio de leurs réserves (l’argent dans leurs coffres) par rapport à l’argent total inscrit dans les comptes des gens, le taux de réserve, soit supérieur au taux minimal. Donnons notre premier exemple concret: Moi, Monsieur Banquier, va voir le gouvernement de mon pays et me fais octroyer une licence pour partir ma propre banque: Grôssbanque. Je ne suis pas bien riche mais il me reste 100$ de mon remboursement de taxes du gouvernement que j’utilise comme capital de base pour Grôssbanque: Grôssbanque a un réserve d’argent de 100$. Le lendemain, Mlle. Entrepreneuse vient à mon bureau pour faire un emprunt pour démarrer son entreprise. Comme le taux de réserve minimal est de 10% et que j’ai une réserves de 100$ et que 10% de 1000$ est 100$, j’ai le droit de prêter jusqu’à 1000$ à Mlle. Entrepreneuse. Je lui fais donc une offre super concurrentielle: je lui prête 1000$ pour 2 ans à un taux d’intérêt de 7% annuel payable annuellement. Ainsi, je sort le livre comptable de Grôssbanque et sous la colonne «compte chèque de Mlle. Entreprise» j’inscris 1000$. Il va s’en dire que je ne paie pas d’intérêt sur les comptes chèque. Je vends ensuite un carnet de chèque à Mlle. Entrepreneuse pour 10$, j’ai donc maintenant 110$ de réserve. Mes réserves sont de 110$ et le total d’argent inscrit dans les comptes des gens est de 1000$, le ratio est donc 11% ce qui est supérieur au 10% minimal, je pourrais donc faire d’autres prêts. Bien entendu, je viens de prêter, 1000$ à Mlle. Entrepreneuse mais ces 1000$ n’existaient pas avant, je les ai inventé de toutes pièces. Mais c’est pas trop grave, tant que Mlle. Entrepreneuse n’essaie pas de sortir plus que 110$ de son compte, elle ne se rendra compte de rien. Et au pire, même si elle veux retirer plus de 110$, je peux toujours me tirer d’affaire en empruntant l’argent nécessaire à la banque centrale à un taux d’intérêt annuel de 5%, je sort donc toujours gagnant (Mlle. Entrepreneuse, n’étant pas une banque, n’a malheureusement pour elle et heureusement pour moi, pas le droit d’emprunter directement à banque centrale). Aussi, j’essaie de minimiser la propension de Mlle. Entrepreneuse à retirer de l’argent en chargeant des frais relativement élevés pour ces transactions, cela l’encourage de payer par chèque. D’ailleurs, deux jour plus tard un M. Fournisseur vient chez Grôssbanque avec un chèque de 200$ tiré sur le compte de Mlle. Entrepreneuse car il lui a vendu de l’équipement pour son entreprise. Tant bien que mal, je réussi à le convaincre de ne pas retirer les 200$ (que je n’ai pas) tout de suite mais de plutôt ouvrir un compte Super-méga-ultra-épargne chez Grôssbanque payant un intérêt annuel faramineux de 3% payable annuellement. Je sort donc encore une fois le livre comptable de Grôssbanque et je modifie l’entrée sous «compte chèque Mlle. Entrepreneuse» à 800$ et je commence une nouvelle colonne, «compte épargne M. Fournisseur», sous laquelle j’écris 200$. Mes réserves sont alors toujours 110$ et le total d’argent dans les comptes des gens est de 200$ + 800$ = 1000$, le ratio est donc toujours 11%, j’ai donc des réserves excessives comme on dit. Un ans passe sans qu’il n’y ait plus aucune transaction dans ces comptes. À la fin de l’année Mlle. Entrepreneuse me doit 70$ = 7% de 1000$ en intérêts et je dois 6$ = 3% de 200$ à M. Entrepreneur. Je ressorts donc le livre comptable et je change le montant sous la colonne «compte chèque Mlle. Entrepreneuse» à 730$ et le montant sous la colonne «compte épargne M. Fournisseur» à 206$. Au bout de la première année donc, j’ai fais un profit de 74$ (=10+70-6) sur un capital initial de 100$ en prêtant 1000$ qui n’avait jamais existé. C’est pas mal quand même! Et ce qui est encore mieux, c’est que mes réserves sont toujours 110$ mais le total de l’argent inscrit dans les comptes des gens est de 730$ + 206$ = 936$ et donc le ratio,le taux de réserve, est de 11,8%, je pourrais donc créer et prêter encore 164$ pour ramener mon taux de réserve à 10%. Dans un an encore, Mlle. Entrepreneuse me devra 70$ d’intérêts plus 1000$ pour repayer son prêt initial mais comme elle n’a que 730$ dans son compte chèque, elle devra trouver ailleurs (les profits de son entreprise peut-être) les 340$ restant pour me les donner. Si elle n’est pas capable de payer je pourrai peut-être lui fournir un autre prêt pour qu’elle puisse payer son prêt antérieur, mais cette fois si à un taux d’intérêt plus élevé car elle aura une mauvaise cote de crédit.

En fait, je vous ai menti un petit peu dans le dernier exemple, car seulement les comptes en banque considérés comme «liquides» doivent être pris en considération dans le calcul du ratio, cela veut dire que les comptes d’épargne ne sont généralement pas compris dans ce calcul, donc le compte de M. Fournisseur n’a pas besoin d’être inclus. Donc, après la première année le taux de réserve serait vraiment 110$/730$ * 100% = 15% et Grôssbanque pourrait en effet créer et prêter 364$ de plus à la place de 164$ de plus afin de ramener le taux de réserve au taux minimal de 10%! Dans le prochain exemple, pour se simplifier la vie, on fait comme si les comptes d’épargnent étaient pris en compte dans le calcul du taux de réserve. Dans la table 2 (source: [2] ) ci-bas on voit les vrais taux de réserves moyens de différents pays au cours du temps.

TABLE 2:

	Taux de réserves	moye	ns
	Pays	1968	1978	1988	1998
	Royaume-Uni	20.5	15.9	5.0	3.1
	Turquie	58.3	62.7	30.8	18.0
	Allemagne	19.0	19.3	17.2	11.9
	États-Unis	12.3	10.1	8.5	10.3

Autres parties de la série: Introduction, Partie I, Partie II, Partie III, Partie IV
ERRATUM: Le taux de réserve minimal pour le RU est en fait pas exactement 0 mais 0,35% mais ce taux est purement symbolique puisque les banques gardent en fait un taux bien plus élevé (1-2%) afin de pouvoir répondre à la demande des gens qui veulent retirer de l’argent comptant.

sources:

1. http://en.wikipedia.org/wiki/Fractional_reserve_banking
2. http://en.wikipedia.org/wiki/Reserve_requirement
3. http://en.wikipedia.org/wiki/Local_currency
4. http://fr.wikipedia.org/wiki/Banque_du_Canada#Histoire
5. http://en.wikipedia.org/wiki/Bank_of_Canada#History
6. http://en.wikipedia.org/wiki/Royal_Canadian_Mint
7. http://en.wikipedia.org/wiki/Full-reserve_banking#Monetary_reform
8. http://fr.wikipedia.org/wiki/Cr%C3%A9dit_social
9. http://fr.wikipedia.org/wiki/Finance_islamique
10. http://en.wikipedia.org/wiki/Islamic_banking#Principles
11. Lois sur la Banque du Canada

.

Le système bancaire à réserve fractionnelle: la privatisation de l’argent (partie II)

17 09 2007

Ceci est la deuxième partie d’une série d’au moins trois articles. La première partie est ici. Cette partie est plus technique (et peut être sautée sans perdre trop de l’aspect qualitatif de la chose) mais n’est pas vraiment plus difficile, il suffit d’un peu plus de patience. Dans cet article, on reprend, généralise et étend l’exemple de la partie I aux transactions bancaires les plus communes. Dans le prochain article (partie III) on parlera de l’inflation dans un système bancaire à réserve fractionnelle et d’un peu d’histoire.

Second exemple: plus technique et plus mathématique mais quand même relativement facile

Maintenant prenons notre banque préférée, la banque Grôssbanque. En décembre 1949 la banque Grôssbanque a imprimé un gros billet de R$ (un gros chiffre) et l’a ensuite converti en beaucoup de billets de 100$ et en argent électronique (des «blips» dans l’ordinateur de la banque centrale au nom de Grôssbanque, librement convertibles en argent papier) auprès de la banque centrale tout à fait légalement. Grôssbanque a donc R$ qui lui appartient, mais elle a aussi, grâce aux dépôts de ses dépositeurs (c’est-à-dire les gens qui ont un compte en banque chez Grôssbanque), D$ dans ses coffres forts. Grôssbanque a donc une réserve d’argent de (R+D)$ (cases jaunes dans le Tableau I). Grôssbanque veut faire de l’argent, elle veut donc prêter un maximum d’argent pour un gagner un maximum d’intérêt dessus. Combien d’argent Grôssbanque peut-elle prêter au maximum? Naïvement on croirait que ce serait R$, l’argent qui lui appartient, ou en tout cas, certainement rien de plus que (R+D)$ l’argent qu’elle entrepose dans ses coffres forts. Éh bien non. Grôssbanque peut prêter beaucoup plus que ce qui lui appartient ou que ce qui est déposé dans ses coffres: Grôssbanque peu prêter tant que les réserves de ses coffres forts représentent plus de T% de ses obligations envers ses clients. Autrement dit, si M$ est le montant maximal que peut prêter Grôssbanque, alors on a que:

T = (R+D)/(M+D) * 100

car l’argent que Grôssbanque doit rendre disponible à ses clients est le M$ qu’elle leurs prête et les D$ qu’ils ont déposé eux-mêmes dans leur compte chez Grôssbanque et l’argent qui est en fait disponible à Grôssbanque est le R$ qui lui appartient et les D$ que ses clients lui ont «prêté». La loi requiert alors que le ratio de ces deux quantités soit d’au moins T%. On peu réécrire l’équation d’en haut comme suit:

M = (100/T)*R + (100/T-1)*D

Donc si T est inférieur à 50 (ce qui est le cas pour la majorité des pays), on aura bien que M, le montant d’argent maximal que peux prêter la banque est supérieur à R+D, l’argent qu’a la banque dans ses coffres! Par exemple, pour T = 10% comme aux États-Unis on a M = 10*R + 9*D! La banque crée donc de l’argent qui n’existait pas avant! Notons par ailleurs que plus T est petit, plus la banque peut créer de l’argent. Si T = 0 (un taux minimal de réserve de 0%) cela veut dire que la banque peut créer et prêter autant d’argent qu’elle le veut, indépendamment de l’argent qu’elle possède vraiment ou de l’argent déposé chez elle par des dépositeurs, c’est la situation au Canada depuis 1994.

Pour ce qui suit, nous utiliserons des mini-simili-tableaux-comptables où sont comptabilisées chaque transactions. Notons que le mot passif indique une dette donc, dans la colonne «peuple passif» on inscrit tout ce que le peuple a de dette. Le mot actif indique un avoir, une possession. Et donc l’avoir net du peuple (la case rouge) est le total de la colonne actif moins le total de la colonne passif. Pour Grôssbanque, on a la même chose, ce qu’elle possède est dans la colonne actif et ce qu’elle doit est la colonne passif. Notons ici que pour ce qui est des cases jaunes, l’argent que tient Grôssbanque, la case jaune foncée (brunâtre/kaki) contient l’argent qu’elle est obligé de tenir «dans ses coffres» afin de maintenir son taux de réserve minimal et la case jaune pâle consiste en l’argent «excessif».

Dans ce qui suit, nous allons chercher à calculer l’argent total qui existe au pays. Comment fait-on cela? Premièrement on doit prendre note que l’argent disponible dans le système, c’est le total de l’argent qui peut être utilisé pour acheter des choses. Mais avec quoi peut-on acheter des choses? On peut acheter des choses avec de l’argent comptant détenu par le particuliers, donc le montant dans la case rose fait parti de l’argent total, on peut acheter des choses avec l’argent dans son compte en banque, donc la case bleue fait parti de l’argent total du système, les réserves minimales de la banque ne peuvent pas être utilisées pour acheter des choses car elles doivent rester dans les «coffres de la banque», donc la case jaune foncée ne contribue pas à l’argent total du système, la case jaune pâle par contre est «l’excédant de réserves» de la banque, elle peut donc en disposer comme elle l’entend, donc la case jaune pâle contribue à l’argent total du système. Notons que toutes les cases dans les colonnes «passif» sont des dettes, donc on ne peut pas acheter des choses avec ça, elles ne contribuent donc pas à l’argent total du système. Notons aussi que même si elles sont des dettes, ces cases jaunes n’enlèvent pas d’argent du système (sauf au moment où elles sont repayées). En effet, si Marie Tremblay a une hypothèque restante de 30000$ et a aussi 30000$ dans son compte en banque, elle peut quand même acheter une voiture de l’année à 30000$, elle n’a donc pas zéro dollars mais bien 30000$ et une dette de 30000$. Par contre, comme un le verra plus tard, si à la place d’acheter sa voiture de l’année et de donner ses 30000$ à quelqu’un d’autre, Marie repaie son hypothèque, alors pouf, ces 30000$ disparaissent en fumée, 30000$ viennent d’être détruits. Mais revenons à nos moutons, on a donc que l’argent total dans le système, le montant qui peux être utiliser pour acheter des chose est la somme des cases rose, bleu et jaune pâle.

Récapitulons: au tout début Grôssbanque a R$ qui lui appartient et “le peuple” a D$ qui lui appartient en argent comptant.

On a donc la situation du Tableau 1:

Tableau 1:

Dans le tableau 1 on met que l’argent créé par Grôssbanque et la Banque centrale sont zéro, ce n’est pas exactement vrai, mais bon, pour simplifier les choses on fait comme si ce l’était, comme si on commençait à zéro. On fait comme si l’argent qui existe au tout début n’a été créé par personne. L’argent qui peut être utilisé pour acheter des choses est l’argent que le peuple a en comptant et l’argent que Grôssbanque a dans ses coffres. Car vu que Grôssbanque n’a aucune obligation de fournir de l’argent à quiconque, toute son argent est libre est Grôssbanque n’a pas besoin de garder des réserves car (T/100)* 0 = 0. On a donc zéro dans la case jaune foncée et le restant R dans la case jaune pâle. Et donc, l’argent total dans le système est D+R comme on aurait pu s’y attendre naïvement.

Après un bout de temps le peuple décide qu’il veut mettre son argent à la banque. Le peuple sort donc son argent de dessous et de dedans ses matelas et ouvre des comptes chez Grôssbanque où la totalité de son argent (D$) est déposé. Donc, dans le Tableau 2, dans la case rose de l’argent comptant du peuple on met zéro car le peuple n’a plus d’argent comptant et dans la case bleu de ses comptes en banque on met D$.
Tableau 2:

Du côté de Grôssbanque, Grôssbanque a une dette de D$ envers le peuple car le peuple lui a prêté D$. Cette dette paie des intérêts faibles (comptes épargnes) ou nuls (comptes chèques), on met donc D$ dans la case verte de la colonne passif de Grôssbanque. La case verte est ce que Grôssbanque doit au peuple car c’est l’argent qui est dans les comptes en banque du peuple. La case verte et la case bleue contiennent et contiendront donc toujours le même montant. Dans les coffres de Grôssbanque il y a maintenant R$ qui lui apparient et D$ déposé par le peuple, donc (R+D)$ en tout. Le montant total d’argent que Grôssbanque doit mettre à la disponibilité du peuple (l’argent du peuple dans ses comptes en banque) est de D$, donc Grôssbanque doit garder T/100% de ce montant en réserve est peut faire ce qu’elle veut avec le reste. On a donc que les réserves minimales qu’elle doit garder sont de (T/100)*D$, on met donc ce chiffre dans la case jaune foncée. Dans la case jaune pâle on met les réserves totales (R+D) de Grôssbanque moins ses réserves minimale, donc : R+D – (T/100)*D. Et donc l’argent total qui peut être utilisé pour acheter des choses est la case bleue plus la case jaune pâle, c’est-à-dire que l’argent total dans le système est de D+R+(1-T/100)*D = (R+(2-T/100)*D)$. Ceci est plus qu’avant ! Il y a (1-T/100)*D$ de plus créé par la banque. Pour donner une idée concrète de ce que cela représente, si le peuple avait un million de dollars (D=1000000) et si le taux de réserve minimal est de 10% (T=10) alors 900000$ (900 miles dollars) serait créés. Il y a donc eu création d’argent (par la banque) car une partie de l’argent du peuple, (1-T/100)*D$, peut être utilisé deux fois en même temps ! Le peuple peut utiliser ses D$ comme il l’entend, mais Grôssbanque peut aussi utiliser (1-T/100)*D$ de ces D$ pour acheter ce qu’elle veut car Grôssbanque n’a besoin de garder que T% des dépôts de ses client(e)s dans ses coffres. Notons que le taux de réserve, l’argent dans les coffres de Grôssbanque (somme des deux cases jaunes) diviser par l’argent qu’elle doit rendre disponible à ses clients (case verte) est (R+D)/D*100% ce qui est plus de T% donc Grôssbanque peut faire plus de prêts au peuple puisqu’elle a des réserves excessives. Notons aussi que vu que par définition, dans la case jaune foncée, on a le montant de la case verte multipliée par T/100, le taux de réserve sera à T% lorsque l’argent libre de Grôssbanque, la case jaune pâle, est à zéro. Tant qu’il reste de l’argent libre à Grôssbanque, Grôssbanque peut prêter plus d’argent au peuple.

C’est bien le cas présentement, comme nous l’avons précédemment calculer au deuxième paragraphe, Grôssbanque peux prêter M$= [(100/T)*R + (100/T-1)*D]$ de plus au peuple (pour des hypothèques par exemple). Pour ce faire, Grôssbanque écrit simplement un crédit de M$ aux comptes du peuple. Les comptes du peuple, la case bleue, ont donc maintenant (D+M)$ comme on peut le voir dans le Tableau 3. Evidemment, la banque ne prête pas cet argent gratuitement, elle prête à un taux d’intérêt relativement élevé. Le peuple contracte donc ainsi une dette à intérêt élevé auprès de Grôssbanque : les deux cases beiges. La case verte est l’argent que Grôssbanque doit fournir au peuple s’il décide de vider ses comptes en banque chez Grôssbanque, on a donc D+M dollars dans cette case.
Tableau 3:

Mais d’où provient donc les M$ = [(100/T)*R + (100/T-1)*D]$ que Grôssbanque prête ainsi au peuple ? Il y a premièrement les R$ que Grôssbanque possède, mais ensuite il y aussi les (M-R)$ = (100/T-1)*(D+R)$ que Grôssbanque crée de toutes pièces mais qui n’existe réellement pas et donc qu’elle doit «détruire» à un moment donné. Notons que ce montant d’argent est bien plus que le montant d’argent qu’y existait au début : si le taux minimum de réserve est de 10% alors T = 10 le montant d’argent créé de toutes pièces par Grôssbanque est 9*(D+R) donc neuf fois le montant total d’argent initial ! Bien entendu comme, pour Grôssbanque, l’argent qu’elle crée de toutes pièce est pour elle comme une sorte d’emprunt sans aucun frais d’intérêt qu’elle peut prêter à des taux d’intérêts élevés, Grôssbanque est peu encline à détruire cet argent créé de toutes pièces.

Mais qu’arrive-t-il si Marie, une personne du peuple, sort x$ (en argent comptant disons, car si elle donne un chèque ou paie débit rien ne se passe de notre point de vu) pour acheter une maison ? Premièrement si Marie sort x$ comptant, alors elle a x$ en argent comptant (ou «libre») et doit soustraire x$ au montant de son compte en banque (case bleue). Deuxièmement les réserves de Grôssbanque sont aussi diminuées de x$ car Grôssbanque doit puiser dans ses réserves pour donner x$ à Marie, donc Grôssbanque a donc des réserves de (R+D-x)$ . Mais de par la loi Grôssbanque doit maintenir des réserves d’au moins (T/100)*(D+M-x)$ = [D+R-(T/100)x]$. Grôssbanque se retrouve donc dans une situation illégale, ses réserves sont à court de (1-T/100)*x$, ce que le note en mettent (1-T/100)*x dans la case jaune pâle passif. C’est-à-dire que Grôssbanque est dans le rouge pour ce qui est de son Argent «libre». Par définition on définit y comme étant y = (1-T/100)*x afin de se simplifier un peu la vie. Notez bien aussi que comme le peuple a autant d’argent avant que Marie ait retiré de l’argent qu’après mais que Grôssbanque se retrouve avec un déficit de y$ dans son argent «libre» après le retrait cela veut dire qu’en retirant x$ en argent comptant, Marie a entraîné la destruction de y$. Plus concrètement, si Marie a retiré 10 000$ et que le taux de réserve minimal est de 10% alors y$ = 90 000$ et donc Marie aurait forcé la banque à détruire 90 000$ de l’argent qu’elle avait préalablement créé. Vous noterez que dans le Tableau 4. Grôssbanque a en effet créé y$ de moins que dans le Tableau 3.

Tableau 4:

Grôssbanque a alors deux solutions, soit elle emprunte de l’argent d’une autre banque, soit elle emprunte directement à la banque centrale. Comme on suppose ici que Grôssbanque représente l’ensemble des banque du pays, Grôssbanque emprunte y$ de la banque centrale à un taux d’intérêt moyen (plus haut que le taux d’un compte épargne mais plus bas qu’un taux hypothécaire). Grôssbanque emprunte donc cet argent est la laisse dans ses coffres afin de satisfaire à son taux de réserve minimum requis comme on peut le voir dans le Tableau 5. Mais ces y$ que la banque centrale a prêté à Grôssbanque viennent d’être créé par la banque centrale, soit en les imprimant sur du papier pour ensuite les livrer à Grôssbanque ou plus probablement simplement en l’inscrivant dans le système informatique. On rajoute donc y$ = (1-T/100)*x$ aux réserves de Grôssbanque ce qui a pour effet de remettre la case jaune pâle à zéro. Par contre, Grôssbanque contracte une dette de y$ envers la banque centrale, on l’inscrit dans la case orange à intérêt moyen. Notons que les y$ créé par la banque centrale remplacent exactement les y$ détruit lors du retrait par Marie de x$. L’effet global donc de retirer de l’argent à son compte en banque (dans un système de réserve fractionnelle où T n’est pas zéro) est de détruire de l’argent créé par des banques privées et le remplacer par de l’argent créé par la banque centrale. Contrairement à l’argent qu’elle crée elle-même, une banque privée doit payer des intérêts (quoi que moins que le peuple en général) sur l’argent créé ainsi par la Banque centrale. Donc si plusieurs personnes commencent à retirer de l’argent en même temps d’une banque privée cela peut lui coûter très cher (c’est ce qui se passe actuellement avec la banque anglaise Northern Rock) et même si les gens retire assez d’argent pour qui la banque centrale ne veuille plus lui prêter de l’argent alors la banque privée peut faire faillite.

Tableau 5:

Par la suite Marie donne ses x$ en argent comptant à Julie en échange d’une belle maison en Gaspésie. Il n’y a alors aucun changement dans notre Tableau car il n’y pas de transaction entre Grôssbanque et le peuple, seulement un échange entre une personne du peuple et une autre.

Tableau 6:

Évidemment, Julie ne désire pas garder un gros montant d’argent ayant la valeur d’une maison en argent comptant chez elle, donc elle va porter cet argent à la banque, elle dépose donc x$ dans son compte chez Grôssbanque. Ceci a pour effet qu’elle n’a plus d’argent comptant, donc la case rose est remise à zéro. Cela ajoute aussi x$ aux comptes du peuple donc on ajoute x à la case bleu et à la case verte. Et finalement cela rajoute x$ aux réserves de Grôssbanque qui sont donc maintenant de (D+R+y). Comme les réserves minimal que doit avoir Grôssbanque sont de (D+M)*(T/100)=D+R, Grôssbanque a y$ d’argent libre, comme on peu le constater dans le tableau 7.

Tableau 7:

Comme Grôssbanque a y$ d’argent libre, elle peut faire ce qu’elle veut avec cet argent et, par exemple, elle peut repayer sa dette envers la banque centrale. Grôssbanque repaie donc sa dette envers la banque centrale, pour ce faire elle utilise sont argent «libre» et donc la case jaune pâle est remise à zéro. Puis, comme Grôssbanque a repayé sa dette, la case orange est aussi remise à zéro et l’on obtient le Tableau 8 qui est en fait la même chose que le Tableau 3 car on est revenu à la même situation. Les y$ que Grôssbanque donne à la Banque centrale soit sous forme papier soit sous forme électronique sont alors effectivement «détruits» par la banque centrale. Si l’argent était sous forme électronique alors elle est réellement détruite, si l’argent était sous forme papier alors (si l’argent est toujours en bon état) l’argent est tout simplement retiré de la circulation et placé dans un coffre fort pour être entreposé jusqu’au moment ou la banque centrale aura besoin de créer plus d’argent papier, alors la banque centrale pourra sortir cet argent et le mettre en circulation.

Tableau 8:

Maintenant qu’arrive-t-il si Marie arrive à économiser assez d’argent pour payer une partie ou le tout de son hypothèque ? Marie fait un paiement de H$ à la banque. Comment procède-t-on pour effectuer le paiement ? Premièrement, elle paie H$ de ses dettes donc les cases beiges, les dettes du peuple envers Grôssbanque, diminuent de H$. Deuxièmement, elle effectue ce paiement à partir de sont comte bancaire donc H$ est débité de son compte donc on enlève H à la bleu et à la case verte. Mais puisque la case verte a changée, les réserves minimales que doit garder Grôssbanque ne sont plus les mêmes. Les réserves minimales sont maintenant (T/100)*(D+M-H)$ et donc il y a T*H/100$ qui devaient être dans la réserve mais qui sont maintenant «libérés». Et donc globalement, il y a H$ de moins parce que le peuple a perdu H$ en repayant la banque mais la banque a T*H/100$ de plus dont elle peut disposer comme elle veut et donc en somme (1-T/100)*H$ que Grôssbanque avait créé ont été détruits comme vous le constaterai en comparant le Tableau 9. avec le Tableau 8. Et donc si l’hypothèque H de Marie était de 100 000$, et que le taux de réserve minimal est de 10%, en repayant son hypothèque de 100 000$ il y 90 000$ qui sont partis en fumé.

Tableau 9:

Évidemment, Grôssbanque va la reprêter un maximum d’argent à quelqu’un d’autre afin de pouvoir gagner de l’intérêt dessus. Et donc, par exemple, Grôssbanque pourrait prêter H$ (c’est évidemment le maximum qu’elle peut prêter si elle recrée les (1-T/100)*H$ qui viennent de disparaître) à Jean afin qu’il s’achète un voiture de l’année. On retrouve alors exactement la même situation qu’on avait avant que Marie paie son hypothèque comme on peut le constater en comparant les Tableau 10. et 8.

Tableau 10:

Mais notez que si Jean pense que ça va mal au travail et qu’il risque de perdre son emploi ou que son salaire va être coupé ou va stagner alors il ne voudra pas emprunter pour acheter une voiture. Et si Grôssbanque trouve personne pour emprunter plus d’argent alors les (1-T/100)*H$ ne réapparaîtront pas et il y aura réellement moins d’argent dans le système.

C’est pour ça qu’à la télé ou dans les journaux, on parle tant du «sentiment des consommateurs» ou de «l’indice de confiance des consommateurs». Et c’est pour ça qu’on incite subtilement les gens à dépenser et non pas à économiser. Car, dans le système actuel de réserve fractionnelle, même si individuellement chaque individu à avantage à économiser devant une économie ralentissente, si les consommateurs en général sentent que les temps vont être durs et se mettent à économiser et payer leurs dettes au lieu de dépenser et consommer, des sommes massives d’argent vont être détruites (non seulement ça, mais la «vitesse» de l’argent, la vitesse avec l’argent change de mains, diminue, ceci a le même effet que la destruction de l’argent comme nous allons le voir dans la partie III de cette série d’articles). Et qui dit moins d’argent dit une économie qui roule moins vite. Qui dit moins d’argent, dit aussi pas assez d’argent pour acheter tous les biens produits. Les entreprises ont donc le choix entre ne pas vendre leurs produits, ou les vendre en dessous du prix coûtant. Ceci précipitera donc une récession. Cette sorte de récession est ce que les économistes (une bande de crack-potes avec des oeillères plus grosses que la tête) et les médias (soit totalement ignorants, soit décevant intentionnellement les gens) aiment à appeler une «crise de surproduction» (cette expression me fait tellement rire, elle est tellement absurde, elle est pire que le double-speak orwellien et l’absurde d’Ionesco combinés, comment se peut-il que l’on produise trop alors qu’il y toujours pleins de gens dans la pauvreté la plus abjecte, pleins de gens sans nourriture, sans maison, avec que peu de vêtements, alors qu’il y a toujours pleins de gens qui travaille à se briser le dos mais qui arrivent à peine joindre les bouts?!? comment peut-il y avoir surproduction dans de telles circonstances??). La solution dans le système actuel? La destruction des moyens de production: la fermeture d’usines et d’entreprises par la faillite (une partie de leurs équipement et infrastructures se font acheter à rabais par les plus grosses entreprises qui ont assez d’argent en réserve pour survivre la récession (un exemple actuel de ça est l’annonce hier du possible achat de Nothern Rock par HSBC ou Lloyds en Angleterre) mais ne sont pas utilisées dans l’immédiat car les stocks sont suffisant pour satisfaire à la «demande») pour les plus petites qui sont plus vulnérables et la fermeture temporaire des moyens de productions des plus grosses entreprises. Cela «résout» le problème de deux façons: premièrement, la masse d’employé(e)s licencié(e)s ne peuvent plus se permettre «le luxe» d’économiser et de payer leurs dettes (ce qui détruit l’argent), certain(e)s doivent même s’endetter (ce qui crée de l’argent) de nouveau juste pour survivre, deuxièmement, les petites et moyennes entreprises ayant été éliminées il y a moins de produits sur le marché, l’offre et plus faible, il y a donc une sorte de rééquilibrage de l’offre et de la demande, mais plus important encore, les grandes entreprises se trouvent en position de quasi-monopole, elles peuvent donc fixer leurs prix (au dessus du prix coûtant) sans égare au fait que la population en général n’a plus les moyens de payer ces prix (parce qu’il n’y a plus autant d’argent le système), de toute façon, la population peut toujours s’endetter (ce qui crée de l’argent) afin de se loger et de se nourrir. Donc en fait, une récession n’est pas si mal (c’est même très bien), pour les plus grandes entreprises car cela élimine la compétition et leur permet de garder une position dominante, et comme bonus, elles peuvent se rééquiper, augmenter leurs concessions d’exploitations de ressources naturelles (terres agricoles, champs de pétrole, quotas de production, mines, etc.) et agrandir leur infrastructure à peu de frais en achetant les résidus de leurs défuntes compétitrices. Des récessions à intervalles réguliers sont presque essentielles aux grandes entreprises (et banques) afin de préserver leur position dominante, d’ailleurs ces compagnies (mais surtout les banques) ne manquent pas d’inciter régulièrement la banque centrale à provoquer des récessions, et comme les dirigeant(e)s de la banque centrale sont des banquièr(e)s qui ont déjà et qui retournerons sûrement travailler dans le secteur privé les banques privées et les entreprises qu’elles représentes n’ont pas trop de mal à se faire entendre. Mais le plus drôle dans tout ça, c’est qu’on entend souvent dire que le problème de surproduction est inhérent au capitalisme. Strictement parlant c’est totalement faux, ce problème est inhérent au système bancaire que nous utilisons, par exemple, dans un pays où l’on utiliserait un système bancaire de Crédit Social (voir la section «articles de mise en contexte» du blogue) on n’aurait pas de problème inhérent de «surproduction» et ce serait toujours un système capitaliste (dans le sens que les moyens de productions peuvent toujours être de la propriété privée).

Après qu’un an soit passé (ou quelconque période) le temps de verser et de collecter les intérêts est arrivé. Grôssbanque doit payer de faibles (ou pas du tout si c’est un compte chèque) intérêts au peuple sur le montant dans la case verte du Tableau 10. et le peuple doit payer des intérêts élevés sur le montant inscrit à la case beige. Disons que la banque reçoit I$ en intérêts et dois payer i$ en intérêts au peuple. I est un montant supérieur à i sinon la banque ferrait vite faillite et dans la pratique ce nombre est immense. Soit donc P$ = (I-i)$ le montant nette que Grôssbanque reçoit du peuple. Alors le peuple doit payer un montant P$ à Grôssbanque. Comment faire ? La case verte qui est égal à la case bleu est le montant d’argent que Grôssbanque doit au peuple, il suffit donc de soustraire P de ces deux cases. Mais alors, le montant de réserve minimum devient (T/100)*(D+M-P)$= [D+R-(T/100)*P]$ ce qui veut dire que l’argent «libre» de la banque est (T/100)*P. Par contre le peuple a perdu P$ donc globalement il y a eu destruction de (1-T/100)*P$ et la situation est comme illustrée au Tableau 11.

Tableau 11:

Mais évidemment, encore une fois, Grôssbanque voulant maximiser ses profits va prêter autant d’argent qu’elle peut dans la limite du légal. Le montant maximum K$ qu’elle peut prêter est tel que (D+R)/(K+[D+M-P]) = T/100. Ce qui signifie que K = P. Donc Grôssbanque peut (créer et) prêter P$ au peuple. Puisque Grôssbanque prête P$ de plus au peuple, en plus du M$ déjà prêté, on devra ajouter P aux cases beiges. Grôssbanque doit mettre l’argent à disposition du peuple dans leur comptes en banque et donc on doit aussi ajouter P à la case bleu et à la case verte. Pour ce qui de l’argent «libre» de la banque on sait qu’il n’en restera plus car on a choisi de prêter le maximum d’argent. On se retrouve donc avec la situation suivante telle que décrite par le Tableau 12.

Tableau 12:

Et on voit donc qu’au bout du compte, le montant total d’argent est le même qu’avant que les intérêts soient payés sauf que maintenant le peuple est plus endetté et plus pauvre et Grôssbanque est plus riche.

Mais maintenant qu’arrive-t-il si la population du pays augmente et production du pays augmente ? Il y a plus de gens et plus de produit donc on a besoins de plus d’argent dans le système pour pouvoir continuer toutes les transactions quotidiennes au même rythme qu’avant. Comment fait-on pour augmenter le quantité d’argent dans le système ? C’est assez bizarre mais c’est tout de même assez simple. Si la banque centrale décide qu’on doit augmenter la quantité d’argent en circulation, elle crée N$ disons et elle les prête (de façon presque permanente) aux banques privées à un taux d’intérêt moyen. Grôssbanque reçoit donc un prêt de N$ de la banque centrale et donc les réserves de Grôssbanque augmentent de N$ mais aussi ses dettes à intérêt moyen (case orange) augmentent de N$. On se retrouve donc dans la situation du Tableau 13.

Tableau 13:

Évidemment, Grôssbanque ne va pas laisser l’argent se reposer dans ses coffres car elle doit payer de l’intérêt sur cet argent et donc si l’argent reste dans ses coffres à rien faire Grôssbanque va perdre de l’argent. Grôssbanque veut faire comme d’habitude et prêter le plus d’argent possible à un haut taux d’intérêt. La question est donc de savoir combien d’argent Grôssbanque peut prêter au peuple. Les réserves de Grôssbanque sont maintenant (R+D+N)$. Le montant maximal qui K$ qui peut être prêté doit satisfaire à l’équation (R+D+N)/(D+M+K)=T/100 ce qui impose que K = (100/T)*N. Ce qui veut dire par exemple, si T = 10, que Grôssbanque peut prêter 10 fois le montant d’argent qui lui a été prêté par la banque centrale. Ceci veut dire que Grôssbanque crée 9*N$ à partir de rien, totalement gratuitement et ensuite prête cet argent au peuple à des taux d’intérêts élevés. Pour ce qui est du N$ que la banque centrale lui a prêté elle le prête aussi à un taux d’intérêt élevé, plus élevé que le taux moyen auquel la banque centrale lui a prêté. On se retrouve donc dans la situation décrite par le Tableau 14.

Tableau 14:

Ce qui est le plus scandaleux est que, à toute fin pratique, cette méthode de créer l’argent est l’unique méthode utilisée. Ceci veux dire que (si T = 10 mais dans les faits T tourne plus au tours de 2) pour chaque dollars créé par le gouvernement, 9 dollars sont créés par des banques privées. Non seulement ça mais pour créer plus d’argent il faut absolument que quelqu’un quelque part s’endette et donc si un jour toutes les dettes étaient payées il ne resterait presque plus d’argent ! En fait la situation est encore pire que ça parce que pour des pays comme le Canada, l’Angleterre et la Suède, T=0 et donc les banques privées peuvent créer autant d’argent qu’elles le souhaitent. Et pour les autres pays, le taux minimal de réserve ne s’applique pas sur tous les comptes bancaires mais seulement les comptent courants (les comptes chèques) et donc les banque peuvent créer autant d’argent qu’elles le veulent tant que cet argent se retrouve dans des comptent épargne. Les banque doivent seulement satisfaire à la contrainte que R/C >T/100 où R est le montant d’argent que la banque a dans ses coffres, C est la somme des montants de tous les comptes courants de cette banque et T est le taux minimal de réserve.

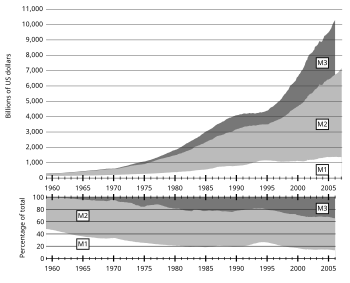
Pour mieux comprendre l’amplitude de l’argent créé par les banques privées regardez le graphique ci-dessous qui se rapporte aux dollars étasuniens. M1 est l’argent «libre» des banques et les comptes courants. M2 est, grosso modo, les M1 plus les comptes épargnes, les comptent d’investissement, etc. et M3 est, grosso modo, M2 plus les dollars étasuniens à l’extérieur du réseau financier étasunien (en Suisse par exemple).

Dans les prochaines parties de la série nous aborderons l’inflation et les cycles économiques.

Autres parties de la série: Partie I, Partie II, Partie III, Partie IV

sources:

1. http://en.wikipedia.org/wiki/Fractional_reserve_banking
2. http://en.wikipedia.org/wiki/Reserve_requirement
3. http://en.wikipedia.org/wiki/Local_currency
4. http://fr.wikipedia.org/wiki/Banque_du_Canada#Histoire
5. http://en.wikipedia.org/wiki/Bank_of_Canada#History
6. http://en.wikipedia.org/wiki/Royal_Canadian_Mint
7. http://en.wikipedia.org/wiki/Full-reserve_banking#Monetary_reform
8. http://fr.wikipedia.org/wiki/Cr%C3%A9dit_social
9. http://fr.wikipedia.org/wiki/Finance_islamique
10. http://en.wikipedia.org/wiki/Islamic_banking#Principles
11. Lois sur la Banque du Canada
12. http://en.wikipedia.org/wiki/Money_supply